Comment choisir la forme de courbe de came des objectifs zoom ?
- Partager
- Heure de diffusion
- 2021/11/5
Résumé
La conception de courbe de came est une étape indispensable dans la conception d’optimisation des zooms infrarouges. Cet article sélectionnera la forme de courbe de came appropriée de l'objectif zoom à travers des exemples et des analyses.

Dans la dernière étape de la conception de l’objectif zoom, la courbe de came doit être conçue. Afin d'équilibrer l'uniformité du changement de grossissement d'imagerie et l'angle de rotation de la came, une forme de courbe de came appropriée doit être sélectionnée, et une certaine relation fonctionnelle entre le grossissement d'imagerie M et l'angle de rotation de la came θ doit être établie.
En fonction des conditions aux limites réelles et de la continuité fonctionnelle que doit respecter la courbe de came, plusieurs relations fonctionnelles communes entre M et θ sont établies et les exemples de conception sont simulés par Matlab.
Les résultats montrent que lorsque la relation fonction puissance établie entre le grossissement d'imagerie M et l'angle de rotation de la came θ et l'angle d'augmentation de la pression ne dépasse pas la valeur admissible, l'équilibre de changement de grossissement variable est le meilleur, la courbe de changement de grossissement est lisse, et il n'y a pas de point d'inflexion de la came. Cette méthode peut aider les concepteurs à modifier la forme de la courbe de came en fonction de différentes exigences de conception et à trouver la meilleure courbe de came de zoom.
Dans le système de zoom, la came est le composant qui contrôle le mouvement du groupe de lentilles et permet au système de modifier la distance focale tout en maintenant la stabilité du plan image. Le fonctionnement fluide, flexible et rapide du zoom constitue un élément important des performances du zoom, qui est directement lié à la rugosité du profil de la came et à l'angle de pression de la courbe de la came.
Si la courbe de came présente un angle d'inclinaison plus grand dans une certaine section, elle apparaît plus raide. Lors de la rotation de la came, vous ressentirez une sensation de main plus lourde. L'engrenage qui entraîne la came en rotation est usé et le bord de la rainure de la came peut même être comprimé et déformé, ce qui affecte la qualité de l'image ; lorsque c'est plus grave, la came sera bloquée et ne pourra plus être utilisée du tout.
Dans l'objectif zoom à compensation mécanique, en sélectionnant la relation de mouvement entre le mouvement du groupe zoom et l'angle de came, il peut être assuré que le grossissement d'imagerie change à une vitesse uniforme ou à une accélération uniforme pendant le processus de zoom. C’est très prometteur, que ce soit pour la télévision, la photographie argentique ou les zooms utilisés dans le suivi militaire.
Mais en même temps, l'angle de pression correspondant à la courbe de came aux deux extrémités des focales longue et courte sera très grand. Lorsqu'on poursuit la miniaturisation de l'objectif zoom, le couple de rotation de la came dépassera souvent la valeur tolérable. Par conséquent, il est nécessaire de choisir la forme de la courbe de came et de trouver un équilibre entre l’uniformité du changement de grossissement d’imagerie et l’angle de rotation de la came.
Cet article établit la relation fonction puissance entre le grossissement d’imagerie M et l’angle de rotation de la came θ. Combinée à l'équation du système de zoom, l'interface de simulation Matlab est écrite pour simuler la forme de la courbe de came. Les résultats montrent que la fonction établie M-θ est plus linéaire que l'ajustement de courbe traditionnel et la méthode θ-x, la courbe de came est plus lisse, l'angle de montée en pression est globalement plus petit (<45°) et le changement de grossissement est plus équilibré. .
La théorie de base du système de zoom
La dernière étape de la conception d'un objectif zoom, c'est-à-dire qu'une fois les paramètres du mécanisme optique (rayon, intervalle, matériau du verre) de chaque élément de l'objectif déterminés, il est également nécessaire de calculer la relation numérique entre le déplacement du groupe zoom et la compensation. groupe pour traiter la piste de came. Ci-dessous, nous discutons des deux formes de l’équation de la courbe de came.
Forme 1 : obtenez la quantité de mouvement du groupe de compensation y à partir de la quantité de mouvement du groupe à grossissement variable x, puis obtenez la courbe de came à grossissement variable, à savoir
x → y → m2* ,m3* →M (1)
Forme 2 : Obtenir les grossissements m2* et m3* du groupe à grossissement variable et du groupe de compensation à partir du grossissement variable M requis par le système, et obtenir le mouvement x, y du groupe à grossissement variable et du groupe de compensation, puis obtenir la courbe de came, à savoir
M→m2*,m3* → x, y (2)
Il ressort des deux formes ci-dessus que pour établir l'équation de la came puis traiter la piste de came, il est nécessaire d'établir la relation fonctionnelle entre l'angle de la came et l'une des variables ci-dessus.
Conception de la courbe de la came de zoom
Afin d’équilibrer l’uniformité du changement de grossissement d’imagerie et l’angle de la came, il est nécessaire de sélectionner une forme de courbe de came appropriée. Cela nous oblige à établir une certaine relation fonctionnelle entre le grossissement d'imagerie M et l'angle de rotation de la came θ, qui sera discutée ci-dessous.
1. Discussion formelle
Tout d’abord, spécifiez les symboles suivants.
F1,F2,F3,F4: Il s'agit des distances focales du groupe fixe avant, du groupe zoom, du groupe de compensation et du groupe fixe arrière ;
m2,m3: Respectivement le grossissement latéral du groupe zoom et du groupe compensation ;
m23=m2m3: Le grossissement latéral de la partie à grossissement variable composée du groupe à grossissement variable et du groupe de compensation ;
m230:Le grossissement horizontal de la partie à grossissement variable au point de départ (θ=0) à la position focale. Cet exemple est la position de distance focale la plus courte ;
L: Le mouvement maximum du groupe de zoom ;
θ : l’angle de rotation de la came ;
α : l’angle de rotation maximal de la came ;
R: Rayon du tambour :
M : grossissement du zoom ;
Max : grossissement maximal du zoom ;
x,y : représentent respectivement la quantité de mouvement du groupe de zoom et du groupe de compensation ;
Parmi eux, kXet kouisont respectivement les pentes du groupe de zoom de la courbe de came et du groupe de compensation, c'est-à-dire la valeur tangente de leur angle de montée en pression.
Lors de la construction de la relation fonctionnelle entre θ et M, il faut prêter attention à deux conditions aux limites :
Condition aux limites 1 : Lorsque θ=0°, M=1
Condition aux limites 2: Lorsque θ=α, M=Mmax
(1) θ a une relation linéaire avec M
Cela peut faire en sorte que le changement de grossissement produise un effet uniforme, cette relation peut être exprimée comme
La formule ci-dessus peut être utilisée pour différencier θ afin d'obtenir le taux de changement de grossissement :
(1) Il existe une relation linéaire entre θ et M
(a) Construisez d’abord la relation de fonction puissance entre θ et M :
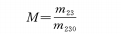
M : grossissement du zoom ;
Mmaximum: Grossissement maximal du zoom ;
x,y : représentent respectivement la quantité de mouvement du groupe de zoom et du groupe de compensation ;
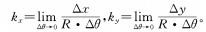
Parmi eux, kXet kouisont respectivement les pentes du groupe de zoom de la courbe de came et du groupe de compensation, c'est-à-dire la valeur tangente de leur angle de montée en pression.
Lors de la construction de la relation fonctionnelle entre θ et M, il faut prêter attention à deux conditions aux limites :
Condition aux limites 1 : Lorsque θ=0°, M=1
Condition aux limites 2: Lorsque θ=α, M=Mmax
(1) θ a une relation linéaire avec M
Cela peut faire en sorte que le changement de grossissement produise un effet uniforme, cette relation peut être exprimée comme

La formule ci-dessus peut être utilisée pour différencier θ afin d'obtenir le taux de changement de grossissement :
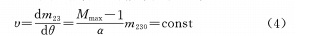
(1) Il existe une relation linéaire entre θ et M
(a) Construisez d’abord la relation de fonction puissance entre θ et M :

Dans la formule, M, Mmaximum, α, θ sont définis comme ci-dessus, n est le coefficient de courbe de came, qui peut également être considéré comme un coefficient d'ajustement, et n≠0 est spécifié. (5) Différencier la formule en θ peut être obtenu :
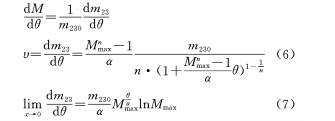
(b) Construire la relation de fonction exponentielle entre θ et M
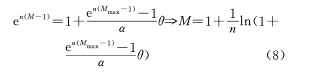
La formule (8) peut être obtenue en différenciant θ :
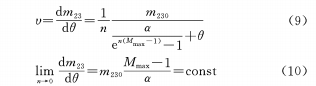
(c) Construire la relation de fonction logarithmique entre θ et M
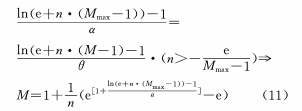
Après différenciation, il y a
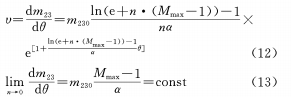
(d) Construire la relation de fonction gaussienne entre θ et M
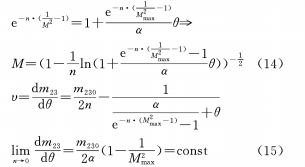
(e) Les quatre relations fonctionnelles ci-dessus sont utilisées dans le cas de n≠0. Pour le cas n=0, on stipule :

Autrement dit, il existe une relation linéaire entre θ et x, qui est actuellement la relation la plus couramment utilisée. Différenciez l'équation (16) et l'équation de la came pour obtenir le taux de variation du grossissement tel que
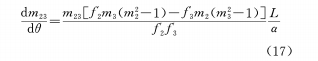
Les résultats ci-dessus sont discutés ci-dessous.
(1) Lorsque θ a une relation linéaire avec M, il ressort de la formule (4) que les temps variables du système et la vitesse uniforme sont très souhaitables. Cependant, en raison de la relation non linéaire entre la quantité de mouvement x du groupe de zoom et M, cela conduira inévitablement à une non-uniformité de la vitesse de mouvement du groupe de lentilles et à un déséquilibre de l'angle de pression.
(2) Lorsque θ et M sont dans une relation non linéaire et que θ et M sont dans une relation de fonction de sauvegarde, si n est constant, le grossissement variable et l'angle de rotation changeront dans une relation de fonction de sauvegarde. Il ressort de la formule (7) que lorsque le coefficient n de la courbe de came s'approche de 0, le grossissement variable et l'angle de rotation changent de façon exponentielle, c'est-à-dire que le grossissement augmente de plus en plus vite pendant la rotation de la came.
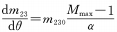
Lorsque n=1 et que les conditions de la formule ci-dessus apparaissent, le taux de changement de grossissement est une valeur fixe, c'est-à-dire pendant toute la rotation de la came depuis la fin de la focale la plus courte jusqu'à la fin de la focale la plus longue. , le changement de grossissement est uniforme, ce qui devient la situation discutée dans la formule (4).
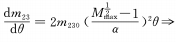
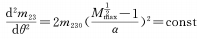
Lorsque m = 1/2 et que les conditions de la formule ci-dessus apparaissent, le changement de grossissement est uniformément accéléré, ce à quoi nous nous attendons également.
(3) La relation entre θ et M est exponentielle, logarithmique et gaussienne. Lorsque n est constant, le taux de changement de grossissement est inversement proportionnel à θ, c'est-à-dire que lorsque la came tourne progressivement de la distance focale la plus courte à la distance focale la plus longue, le taux de changement de grossissement devient de plus en plus lent.
Lorsque n change, le taux de changement du grossissement est non linéaire avec la courbe θ. Lorsque le coefficient n de la courbe de came s'approche de 0, le taux de variation du grossissement est constant, c'est-à-dire que le changement du grossissement est linéaire.
D'une manière générale, le principe de sélection de la courbe de came est de sélectionner la forme de courbe avec le meilleur changement de grossissement variable et une courbe de changement de grossissement fluide lorsque l'angle de montée en pression ne dépasse pas la valeur autorisée.
Grâce à la discussion ci-dessus et à la simulation expérimentale Matlab, nous comprenons que lorsque la relation entre θ et M est une fonction de secours, en sélectionnant le coefficient d'ajustement n approprié, on peut obtenir que lorsque l'angle de pression est proche de la valeur admissible, la variable le changement de grossissement a le meilleur équilibre et le changement de grossissement. La courbe est douce et il n’y a pas de point d’inflexion de came.
Cependant, aucune des autres fonctions ne permet d’obtenir de meilleurs résultats. La figure 1 est un diagramme de simulation de came conçu à l'aide d'un logiciel de dessin tridimensionnel basé sur les résultats de l'analyse précédente. Ce qui suit décrit les résultats de nos expériences de simulation.
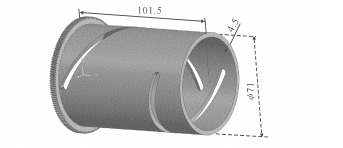
Fig. 1 Figure de simulation de came
2. Analyse et simulation
Combinez les deux formes de méthodes de résolution de courbes de came données ci-dessus et la relation fonctionnelle entre θ et M, pour compiler l'interface graphique Matlab.
Les paramètres d'entrée du programme sont :
Coefficient de courbe de came n, courte focale f du système optique0, distance focale du groupe à grossissement variable f2, distance focale du groupe de compensation f3, avance (distance de déplacement du groupe à grossissement variable de la focale courte à la focale longue) wl, objets du groupe à grossissement variable à focale courte, la distance est l20, la distance d'image du groupe de compensation est ll30en cas de mise au point courte, l'angle de rotation maximal de la came α, l'intervalle d'angle de rotation mu en unités d'angle et le diamètre du tambour à came dd.
Les paramètres de sortie du programme sont :
Angle de rotation, mouvement du groupe de zoom, mouvement du groupe de compensation, distance focale, angle d'augmentation de pression du groupe de zoom, angle d'augmentation de pression du groupe de compensation et données et graphiques de rapport de zoom.
Grâce à cette interface de programme, vous pouvez facilement voir la relation entre le rapport de zoom et l'angle de rotation, observer si l'angle d'augmentation de la pression dépasse la valeur autorisée et modifier le coefficient d'ajustement pour modifier rapidement la relation ci-dessus afin de trouver la meilleure courbe de came requise. .
Prends le 20Xsystème de compensation positive du zoom continu conçu par le groupe de recherche comme exemple pour sélectionner la courbe de came.
Les paramètres fixes sont :
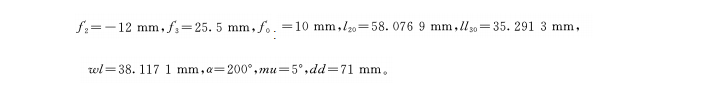
Paramètre variable : coefficient d'ajustement n
Ce programme est modifiable pour tous les paramètres ci-dessus. Afin de faciliter la discussion, nous considérons ici principalement l’influence du coefficient d’ajustement n sur le résultat.
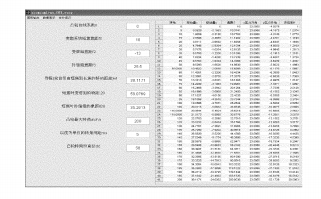
Fig.2 Interface de simulation Matlab
(1) Lorsque n = 0, il existe une relation linéaire entre θ et x, comme le montre la figure 3.
(2) Lorsque n = 0, 047, le graphique de la fonction puissance est illustré à la figure 4.
(3) Lorsque n= 0, 000 1, le graphique de la fonction exponentielle est présenté à la figure 5.
(4) Lorsque n = 2,32, le graphique de la fonction logarithmique est illustré à la figure 6.
(5) Lorsque n = 0,1, le graphique de la fonction gaussienne est présenté à la figure 7.
L'expérience prouve que la discussion précédente sur la relation entre diverses fonctions est cohérente avec l'évolution de la courbe graphique.
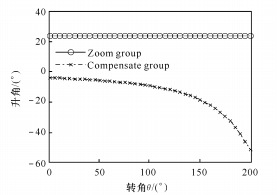
(a) Relation entre l'angle de montée en pression et l'angle de rotation
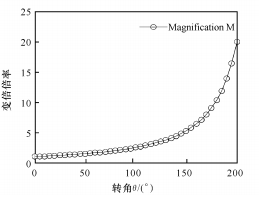
(b) Relation entre le rapport de zoom et l'angle de rotation
Fig. 3 Relation linéaire entre θ et x
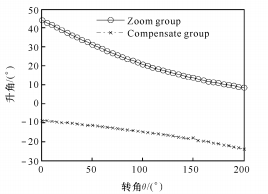
(a) Relation entre l'angle de montée en pression et l'angle de rotation
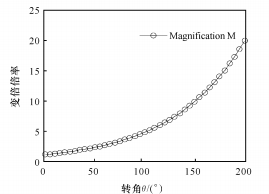
(b) Relation entre le rapport de zoom et l'angle de rotation
Fig. 4 Fonction puissance entre θ et M
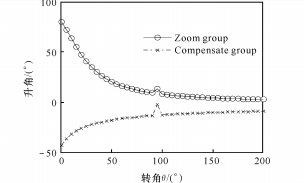
(a) Relation entre l'angle de montée en pression et l'angle de rotation
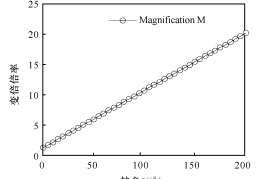
(b) Relation entre le rapport de zoom et l'angle de rotation
Fig. 5 Fonction exponentielle entre θ et M
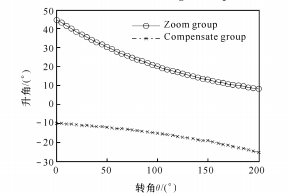
(a) Relation entre l'angle de montée en pression et l'angle de rotation
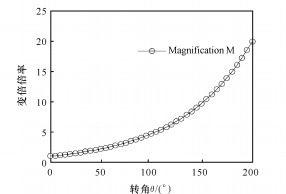
(b) Relation entre le rapport de zoom et l'angle de rotation
Fig. 6 Fonction logarithme entre θ et M
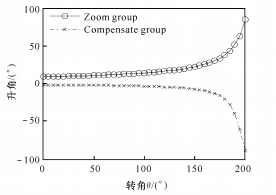
(a) Relation entre l'angle de montée en pression et l'angle de rotation
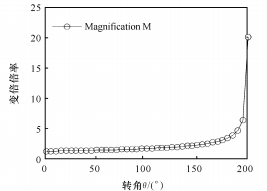
(b) Relation entre le rapport de zoom et l'angle de rotation
Fig. 7 Fonction de Gauss entre Q et M
L'exemple d'analyse ci-dessus illustre brièvement l'influence de différentes valeurs du coefficient d'ajustement n sur les résultats de conception de la courbe de came, et la modification appropriée des paramètres peut obtenir de meilleurs résultats.
Au cours du test, il a été constaté que lorsque n prend certaines valeurs spécifiques, l'angle de pression global de la courbe de came répond aux exigences et seul un certain point dépasse soudainement une valeur raisonnable. Un tel point est ce que nous appelons souvent le point d’inflexion de la courbe, c’est-à-dire le moment où la came tourne. Lorsqu’il atteint un certain angle, il ne peut plus continuer à tourner, c’est-à-dire qu’il reste coincé dans la machine.
Cela est fatal à la fois à la structure de la came et à l'effet de zoom, donc lors de la conception, vous devez éviter les courbes avec de tels points d'inflexion. Autrement dit, plusieurs tests sont nécessaires pour garantir l’obtention d’un coefficient d’ajustement raisonnable.
Dans le même temps, le fait qu'une certaine valeur du coefficient d'ajustement puisse optimiser la courbe de came est lié aux exigences du diamètre de la came, à l'angle de pression de la courbe de came qu'elle peut supporter, aux exigences de l'angle de rotation total de la came. , le volume et le poids du système, ainsi que les exigences en matière de vitesse de zoom.
Par conséquent, le procédé de conception consistant à établir l'équation de la courbe de came de zoom du coefficient d'ajustement peut faciliter la modification de la courbe par les concepteurs de manière flexible, de sorte qu'ils puissent modifier la forme de la courbe de came en fonction de différentes exigences de conception et trouver la meilleure courbe de came de zoom.
Retirez au hasard plusieurs positions de zoom des données expérimentales ci-dessus et amenez-les au Code V pour vérifier que la surface de l'image est stable et que la qualité de l'image répond aux exigences de conception.
3. Résultats expérimentaux
Selon l'analyse et la simulation ci-dessus, la caméra de l'objectif zoom que nous avons conçu a été appliquée avec succès, comme le montre la figure 8. Après une inspection photographique sur le terrain, la caméra conçue en utilisant la théorie ci-dessus dans l'objectif zoom a un zoom rapide et fluide, précis. courbe de compensation, bonne qualité d'image à différents points focaux et répond pleinement aux indicateurs de conception, ce qui vérifie l'exactitude de l'analyse précédente.

Fig. 8 Objectif zoom
Sélectionnez la relation de fonction de puissance entre θ et M, et en modifiant le coefficient d'ajustement n, différents compromis peuvent être faits entre la relation linéaire entre θ et x et la relation linéaire entre θ et m23, ce qui garantit non seulement que l'angle d'augmentation de la pression sera ne soit pas trop important, mais évite également de surmonter la grave non-uniformité de la vitesse de changement de taux.
Bien entendu, afin d'obtenir une relation linéaire de θ-m23 ou θ-dm23/dθ, vous pouvez augmenter l'angle α ou augmenter le diamètre du tambour à came pour réduire l'angle de montée en pression maximum de la courbe de came, mais cela entraînera augmenter le volume et le poids de l'objectif. La diminution de la distance focale du groupe de compensation réduira également l'angle d'augmentation de pression maximum de la courbe de compensation.
Cela compliquera la structure du groupe fixe et réduira même la qualité de la conception optique. Par conséquent, le choix de la relation de fonction puissance entre θ et M peut nous aider à optimiser la courbe de came et à concevoir un objectif zoom miniaturisé de haute qualité.
Si vous souhaitez obtenir plus d'informations sur l'objectif zoom après avoir lu le contenu ci-dessus, vous pouvez contacter Quanhom pour une solution complète.
En tant que fabricant professionnel deComposants opto-électromécaniquesavec de nombreuses années d'expérience, Quanhom est équipé d'une équipe R&D professionnelle et d'un système d'inspection de qualité strict. Nos différentes lentilles infrarouges thermiques (LWIR,MWIR, et caméras SWIR) sont vendus dans le monde entier et ont reçu les éloges et la confiance de nombreux clients. Nous accordons la priorité aux besoins des clients et pouvons leur fournir des services personnalisés et réfléchis. Si vous souhaitez acheter notre objectif à zoom continu infrarouge, veuillez nous contacter immédiatement !
Auteurs : Yan Lei, Jia Ping, Hong Yongfeng, Wang Ping
Source du journal : Vol.31 No.6 Journal of Applied Optics novembre 2010
Date de réception : 2010-03-25 Date de révision : 2010-6-23
Les références:
[1] TANG Jian-bing. Conception optimisée du contour de la came à mise au point variable [J]. Optical Technique, 1994,20(1) : 27- 29. (en chinois avec résumé en anglais)
[2] ZHANG Xiu-li. Une nouvelle méthode pour améliorer le contour de la came de la lentille compensatrice [ J ]. Technique Yunguang, 2003,35 (2) : 16-17. (en chinois avec résumé en anglais)
[3] CUI Jun, SE Guo-Xiong. Conception d'ajustement du contour de la came de l'objectif zoom [J]. Journal chinois des instruments scientifiques, 1990,11 (1) : 107-112. (en chinois avec résumé en anglais)
[4] Groupe de conception d'objectifs de cinéma. La conception optique de l'objectif de photographie cinématographique [ M ]. Pékin : Chinese Industry Publishing Company, 1971. (en chinois)
[5] CHANG Qun. Corpus de conception optique [M]. Pékin : Science Publishing Company, 1976. (en chinois)
[6] CUI Ji-cheng. Conception d’un objectif zoom réfractif-réfléchissant à grande ouverture [J]. Optique et ingénierie de précision, 2008 ? 16 (11) : 2087-2091. (en chinois avec résumé en anglais)
[7] DONG Ke-yan, PAN Yu-long, WANG Xue-jin et al. Conception optique d'un système de zoom progressif double bande infrarouge HDE [ J ]. Optique et ingénierie de précision, 2008 ,16 (5): 764-770. (en chinois avec résumé en anglais)
[8] HAO Hong-yun, XIONG Tao. Système optique à double champ de vision infrarouge à longueur d'onde moyenne [J]. Optique et ingénierie de précision, 2008, 16 (10) : 1891-1894. (en chinois avec résumé en anglais)
[9] CHEN Xin, FU Yue-gang. Conception optimale de la courbe de came pour le système de zoom [J]. Journal d'optique appliquée. 2008, 29 (1) : 45-47. (en chinois avec résumé en anglais)
[10] XU Zheng-Guang, ZHAO Yi-Fei, SONG Cai-Liang et al. Optimisation de la conception de la courbe de came de zoom composée avec OZSAD[J]. Journal d'optique appliquée, 2006,27 (3):203-207. (en chinois avec résumé en anglais)
[11] MENG Jun-he, ZHANG ZHen, SUN Xing-wen. Optimisation de la came d'un objectif zoom [J]. Ingénierie infrarouge et laser, 2002, 31(1): 51-54. (en chinois avec résumé en anglais)