Comment les concepteurs optiques jugent-ils les performances des lentilles optiques ?
- Partager
- Heure de diffusion
- 2022/5/20
Résumé
Bien que les graphiques d'aberration soient utiles pour fournir à un concepteur optique les performances d'un objectif, il s'agit généralement d'un critère objectif pour l'utilisateur ou l'évaluateur de l'objectif. L'article suivant décrit brièvement la méthode utilisée par le concepteur optique pour déterminer les performances d'une lentille optique.

Bien que les graphiques d'aberration soient parfaits pour fournir à un concepteur optique les performances d'un objectif, généralement, en particulier pour l'utilisateur ou l'évaluateur de l'objectif, une norme d'objectif est absolument indispensable.
La fonction de transfert de modulation (MTF) est l'un des critères les plus largement utilisés pour l'évaluation de l'imagerie par lumière incohérente, où l'accent est mis sur le contraste ou la netteté de l'image.
En fait, de nombreuses lentilles optiques modernes sont directement mesurées par les performances MTF.
Comme le montre la figure 1, considérons un système optique imaginant un réseau avec une distribution d'intensité sinusoïdale. Pour l'imagerie en lumière incohérente, l'intensité de l'image est également sinusoïdale, mais le contraste est réduit.
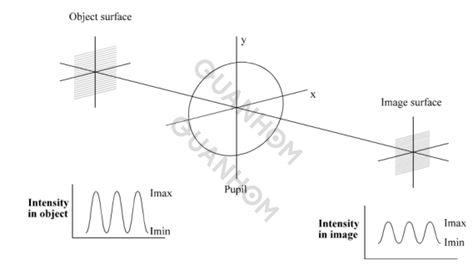
Figure 1 Comparaison d'images d'objets d'un système optique
MTF est le contraste de l'image divisé par le contraste de l'objet ; évidemment, c'est une fonction de la fréquence spatiale, et les tracés de la FTM en fonction de la fréquence spatiale (généralement en « paires de lignes/mm ») sont souvent utilisés dans la conception optique.
La fonction de transfert optique est définie comme :

À proprement parler, il faut faire la distinction entre la fonction de transfert optique (OTF) et la fonction de transfert de modulation (MTF).
L'OTF est un vecteur qui inclut la phase et l'amplitude de l'image, où l'amplitude est la MTF.
En fait, la principale considération dans la conception optique est la FMT. Le terme de phase, parfois appelé fonction de transfert de phase (PTF), représente l'écart de l'image sinusoïdale réelle par rapport à l'image sinusoïdale idéale, exprimé en fonction de l'angle de phase en fonction de la fréquence spatiale. Si la phase dépasse 180°, la FTM peut être négative. Cela représente une inversion de phase, qui se traduit par une inversion du contraste de l'image. En réalité, cela peut se produire aux hautes fréquences de nombreux objectifs.
1. Théorie
Pour les systèmes éclairés par une lumière incohérente, la FMT peut être obtenue en utilisant la transformée de Fourier de la fonction d'étalement des lignes. Habituellement, le MTF est obtenu de cette manière.
Cependant, l'OTF de diffraction peut être rapidement résolue en utilisant l'intégration d'autocorrélation :
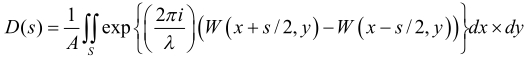
où D(s)=OTF, A=zone de pupille lumineuse, S est la zone de chevauchement des deux pupilles lumineuses, W est l'aberration du front d'onde, S est la fréquence spatiale simplifiée égale à fλ/NA et NA est l'ouverture numérique.
2. approximation géométrique
Dans l'approximation d'optique géométrique, nous supposons que λ est proche de zéro, donc la FTM (dans la direction méridionale) est :
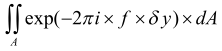
Il s’agit de l’intégration de l’élève dans son ensemble, qui en pratique peut être approchée par une simple sommation.
3. La vraie solution
Parce que nous avons besoin de connaître non seulement la direction sagittale mais aussi la FTM dans la direction méridionale, la FMT dans la direction sagittale est résolue par la formule suivante :
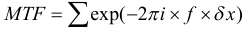
La FTM dans le sens méridien est obtenue par la formule suivante :
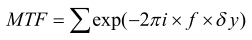
Il est pratique de tracer de nombreux rayons lumineux (souvent plus de 100), mais seuls les rayons qui traversent réellement le système sont pris en compte pour le calcul de la sommation. Nous traçons également des rayons de plusieurs longueurs d'onde, et les longueurs d'onde peuvent être pondérées différemment lors de la sommation. Il est facile d'ajouter un facteur de correction à la FTM géométrique en multipliant la FTM géométrique par la FTM de diffraction du système idéal. Un tel résultat permet à la FTM géométrique d'être précise à la fois dans les systèmes à grande aberration et dans les systèmes à petite aberration.
Cependant, pour des aberrations modérées, la MTF géométrique donne généralement des résultats décevants. Maintenant, nous devons décider combien de rayons annulaires tracer. En prenant les rayons de la manière indiquée sur la figure 2, on peut voir que les aires de toutes les petites surfaces du demi-cercle sont égales. Il est facile de voir que s’il y a n anneaux de rayons, le nombre total de rayons est de 2n. Lorsque le système optique est symétrique (symétrique par rapport au plan méridien y), pour gagner du temps, le programme n'a pas besoin de calculer les rayons dans la direction x négative.
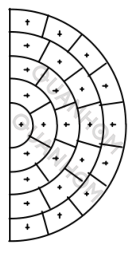
Figure 2. Méthode de prise de ligne pour calculer la FTM géométrique
4. Limite de diffraction
Lorsqu'une lentille avec une ouverture pupillaire finie forme des images d'un objet sinusoïdal, la fréquence limite de sa FMT de diffraction est :
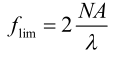
Par exemple, pour un objectif f/2 avec une ouverture numérique NA de 0,25, lorsque la longueur d'onde λ est de 0,0005 mm, la fréquence de coupure est :
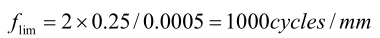
Cette fréquence correspond à un réseau de période spatiale de 0,001 mm (1μm), mais notons que la valeur MTF correspondant à cette fréquence est nulle. Pour 500 / cycles mm, la FMT d'un objectif idéal est d'environ 40 %, donc f/2 est une fréquence plus réaliste.
5. MTF dans ZEMAX
Le MTF utilisé dans ZEMAX fonctionne à la fois comme outil d'évaluation et comme outil d'optimisation.
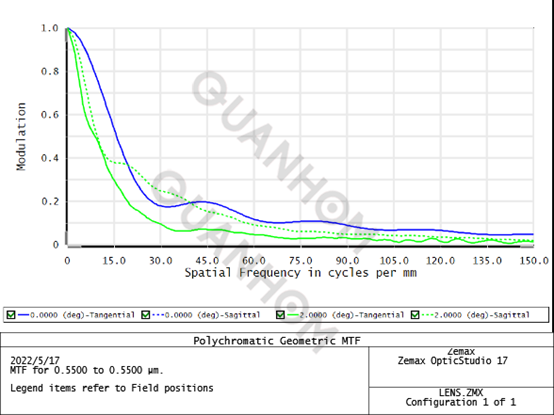
Dans la figure ci-dessus, il y a au total quatre courbes, dont deux sont des courbes MTF méridionales et les deux autres sont des courbes MTF sagittales. Dans le champ de vision 0°, la courbe méridionale MTF et la courbe sagittale MTF coïncident ; et dans le champ de vision 2°, la courbe méridionale MTF et la courbe sagittale MTF sont assez différentes. En effet, le PSF devient asymétrique lorsqu'il est hors axe, ce qui entraîne une différence dans la largeur et le profil du PSF ainsi que dans les directions méridionale et sagittale. Ainsi, une convolution avec l'image paraxiale (ou géométrique) entraînera un delta dans les deux sens. Cela signifie également que la résolution est différente dans ces deux directions.
Ce qui précède décrit brièvement la méthode d'évaluation des performances des lentilles optiques.
QUANHOM est un fabricant de lentilles optiques sur mesure . Notre équipe comble l’écart entre des performances supérieures et un budget limité, surtout lorsque nous sommes impliqués dans des projets intégrant de la haute précision. Les produits comprennent des ensembles optiques infrarouges pour VIS/SWIR/MWIR/LWIR, des oculaires, des éléments de lentilles infrarouges (de monoscopiques à commutation rapide entre les lentilles infrarouges multi-champs et à zoom continu), etc. Nos experts expérimentés et inspirés sont toujours en mesure de fournir une IR optimisée. verre de lentille et options d'assemblage optomécaniques et optoélectroniques.